试验误差相关说明

(一)绝对误差和相对误差

由于试验误差(特别是偶然误差)在所难免，科学实验和生产及商业检验都允许试验存在一定的误差。在综合考虑了生产或科研的要求、分析方法可能达到的精密度和准确度、样品成分的复杂程度和样品中待测成分的含量高低等因素的基础之上提出的可以接受的最大误差数值称为合理的允许误差。所以，不论误差来源如何，误差的大小是最关键的。

在分析实验中，误差的大小可用绝对误差(Ea)与相对误差(Er)两种方式表示。

绝对误差    绝对误差＝测量值-真值                    即Ea=X-T

相对误差    相对误差＝100 (测量值-真值)/真值    即Er =(Ea/T)×100%

例如，在使用常量滴定管进行一次滴定后，有三位学生分别读得消耗的滴定液为10.00、10.01和10.02mL(最后一位小数是估计值)，假如真值是10.01mL，那么这批数据的个别测定误差范围计算如下：

个别测定绝对误差范围＝±0.01mL

然而，这批数据的平均测定绝对误差和平均测定相对误差均为零。这说明，仅从平均测定绝对误差和平均测定相对误差的大小，不能看出一组平行测定的精密度。为反映一组平行测定数据的精密度，需用到偏差。

(二)平均偏差与标准偏差

1．平均偏差

平均偏差又称算术平均偏差，用来表示一组数据的精密度。

平均偏差：

式中X—某次测定数据；

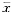—一组平行测定数据的平均值；

n—平行测定次数。

优点：计算简单，可粗略表示一组平行测定数据的精密度；缺点：该组测定中各次测定偏差的大小差异得不到应有反映。

2．标准偏差

标准偏差又称均方根偏差。标准偏差的计算分两种情况：

(1)当测定次数趋于无穷大时标准偏差：

式中u—无限多次测定的平均值(总体平均值)。

即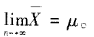：当消除系统误差时，u即为真值·

(2)当有限测定次数时标准偏差：

相对标准偏差(变异系数)：

从数学上看，标准偏差的大小既决定于各次测定是否存在偏差，又决定于各次测定偏差之间的大小差异，大的偏差比小的偏差对标准偏差影响更大。因此，用标准偏差比用平均偏差表示测定偏差更科学、更准确。

例如，对下列两组平行测定数据，分别计算出平均偏差和标准偏差比较。

X-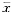: 0.11，-0.73，0.24，0.51，-0.14，0.00，0.30，-0.21

n＝8   d₁＝0.28 S₁＝0.38

X-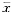；0.18，0.26，-0.25，-0.37，0.32，-0.28，0.31，-0.27

n＝8   d₂＝0.28   S₂＝0.29

可见：d₁=d₂，而：S₁＞S₂

3．平均值的标准偏差

若m个n次平行测定的平均值为：

由统计学可得上列m个数据的标准偏差(平均值的标准偏差)S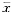与n次平行测定的标准偏差S之间的关系：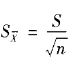

S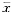又称为标准误，它在表示分析结果时用到。

由S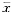/S-n关系曲线(如图1-3所示)可知：

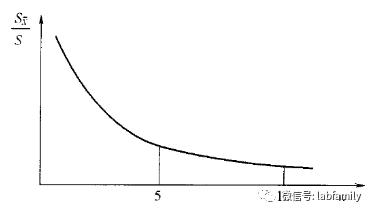
图1-3  S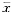/S-n关系曲线

当n大于5以后，曲线变化趋缓；当n大于10以后，曲线变化不大。所以n大于5时，可以用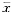±S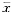的形式来表示分析结果。

例：水垢中Fe₂O₃的质量分数6次测定数据为：79.58%，79.45%，79.47%，79.50%，79.62%，79.38%。计算得出：

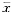=79.50%    S=0.09%    S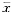=0.04%

则分析结果为：水垢中Fe₂O₃的质量分数=79.50％±0.04%

根据置信度和置信区间知识，用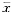±tS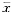表示的结果更合理、更科学。因为用这种方式表示的结果是在一定置信度下真值所处的范围(无系统误差时)。

4.不确定度

不确定度表示由于测量误差的存在而对被测量值不能肯定的程度。此参数表明测量结果的分散程度，是一个正数，它反映了测量结果中未能确定的量值的范围。不确定度按误差性质可分为随机不确定度和系统不确定度，一种性质的不确定度也可由不同分量组成。不确定度的估计方法可分成两类：用统计方法对多次重复测量结果计算出的标准偏差为A类标准不确定度，以u_A 表示，用其他方法估计出的近似“标准偏差”为B类标准不确定度，以u_B表示。用合成方差的方法将各分量合成所得的结果称为合成不确定度(例如将不同标准不确定度各分量用这种方法合成后的结果称标准不确定度，以u表示)，合成不确定度乘以某一合理的正数后称为扩展不确定度(又称总不确定度，以U表示)。不确定度具有概率的概念，标准不确定度的置信概率为68.27%(按正态分布概率计算)，而总不确定度的置信程度应该与之相等或更高。若需要更高，则应乘一因子(称为置信因子)，这正是由合成不确定度计算总不确定度时应该所乘的那个正数。从而得出总不确定度，此时所乘的置信因子通常必须说明。

A类不确定度的计算方法如下：

对于一次进行的n个平行测定的结果，如果已排除了系统误差，规定用标准误来表征A类标准不确定度分量的数值。

当n足够大时，每一测定结果出现的概率服从正态分布，A类不确定度的置信概率为68.3%，u_A就以标准误表示：

u_A＝S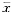

当n只是个位数时(平行测定个数只有几个时)，每一测定结果出现的概率服从t分布，A类不确定度的置信概率为68.3%，u_A就以下式表示：

u_A=tS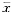

式中t—置信因子，在这里被称作校正系数，可根据n和要求的显著性因子在t分布表中查出该值。对于常规分析，在查该值时，通常采用置信概率P =95％或显著性因子a=0.05。

B类不确定度通常是只考虑仪器的精密度或稳定性问题引起的随机误差，其值近似为仪器测量的极限误差△_B与该仪器测量随机误差的统计分布规律所对应的分布因子K_B之商。

如果某次测量的平行测定个数很多，而误差的数值相差不大，可将其分布视为正态分布，一般取K_B=2或K_B=3。如果某次测量的平行测定个数不多，且仪器测量时，其测量读数在一定区间基本为一个定值，那么其误差分布为均匀分布。一般取。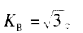

仪器测量的极限误差△_B是指实验中所涉一及仪器引起的最大误差，一般情况下可直接取仪器出厂检定书或仪器上注明的仪器的误差。即

△_Bj=△_仪

在各不确定度分量彼此独立情况下，合成不确定度u的计算方法如下：

设测量结果的不确定度的A分量和B分量分别独立且彼此独立，则合成不确定度为：

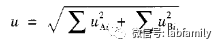
式中u_Ai—u_A的第i个分量；

u_Bi—u_B的第i个分量。

最后应当说明，在分析领域，不确定度的应用目前还不如误差的应用广泛，但在某些分析领域，它有逐渐取代误差的趋势。